# GCD and LCM

GCD:
gcd(a, b):
if b is 0: return a
else return gcd(b, a - b * (a/ b))


The greatest common factor, or GCF, is the greatest factor that divides two numbers. To find the GCF of two numbers:

1. List the prime factors of each number.
2. Multiply those factors both numbers have in common. If there are no common prime factors, the GCF is 1.

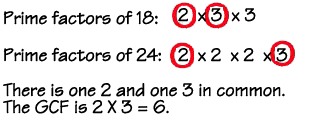
LCM:
lcd(a, b):
return abs(a * b) / gcd(a, b)


The least common multiple (LCM) of two numbers is the smallest number (not zero) that is a multiple of both.

# Another Question is to find the LCM for an Array
http://www.careercup.com/question?id=7937661
http://stackoverflow.com/questions/185781/finding-the-lcm-of-a-range-of-numbers

You can compute the LCM of more than two numbers by iteratively computing the LCM of two numbers, i.e.

lcm(a,b,c) = lcm(a,lcm(b,c))

to prove: basically LCM(a, b) takes the maximum index in the prime factorization of a, b. LCM(a, b, c) takes the maximum index of all possible primes in a, b, and c, which is equivalent to finding the maximum index of primes from a, b and then c.
Based on these, and the fact that LCM(a, b) = a * b / GCD(a, b), we can do an iterative algorithm that only requires a GCD procedure, which can be easily done using the Euclid's algorithm.


GCD and LCM
http://www.boost.org/doc/libs/1_46_0/libs/math/doc/gcd/html/index.html