Tree Balance

When doing the tree balance, the first thing is to know "tree rotation"

Tree rotation - Wikipedia, the free encyclopedia
http://en.wikipedia.org/wiki/Tree_rotation

In the illustrated method in wiki:
OS: denote the side where we want to do the rotation -- original side -- in the example -> left side
RS: denote the purpose side that we are going to move to ---  in the example --> right side

Pivot = Root.OS       ( let Pivot point to P )
Root.OS = Pivot.RS    ( P->right, which is B is assigned to Q->left )
Pivot.RS = Root       ( Q is assigned to P->right )
Root = Pivot          ( Now, P becomes Root ) 

- When a subtree is rotated, the subtree side upon which it is rotated decreases its height by one node while the other subtree increases its height. This makes tree rotations useful for rebalancing a tree.

- When rotating the tree, the in-order traverse will not be changed:

Lefttree:((A, P, B), Q, C) Right tree: (A, P, (B, Q, C))

- To balance the tree: After rotation, the side of the rotation (destination side: RS) will increase its height by 1, while the original side (OS) will decrease its height by 1. So, one can strategically apply rotations to nodes whose left child and right child differ in height by more then 1 ( by compute the tree balance index), whereby the self-balancing tree will be helpful/
http://en.wikipedia.org/wiki/Self-balancing_binary_search_tree

Other Refs:
http://stackoverflow.com/questions/133610/balancing-a-binary-tree-avl
www.cs.princeton.edu/~rs/AlgsDS07/09BalancedTrees.pdf

# Several "Balanced" Tree 
self-balancing tree   http://en.wikipedia.org/wiki/Self-balancing_binary_search_tree

Implementations

Popular data structures implementing this type of tree include:

• AA tree
• AVL tree                         --> Important
• Red-black tree                --> Important
• Scapegoat tree
• Splay tree
• Treap

# 2-3-4-trees

2-3-4 tree. Generalize node to allow multiple keys; keep tree balanced.
Perfect balance. Every path from root to leaf has same length.

Allow 1, 2, or 3 keys per node.
2-node: one key, two children.
3-node: two keys, three children.
4-node: three keys, four children.
(Note that when adding node, -- will have splitting problem)

Search.
 - Compare search key against keys in node.
 - Find interval containing search key.
 - Follow associated link (recursively).


# Red-black trees

http://en.wikipedia.org/wiki/Red_black_tree

http://stackoverflow.com/questions/3270543/red-black-tree-for-sorting

http://stackoverflow.com/questions/2573261/red-black-tree-construction

To construct the Red-black tree

http://ocw.mit.edu/OcwWeb/Electrical-Engineering-and-Computer-Science/6-046JFall-2005/VideoLectures/

Note that, when inserting, always insert new node as black node and then proceed to the necessary correction (repainting and /or rotating)

# B-trees

B-Tree. Generalizes 2-3-4 trees by allowing up to M links per node.

Main application: file systems.
Reading a page into memory from disk is expensive.
Accessing info on a page in memory is free.
Goal: minimize # page accesses.
Node size M = page size.

Space-time tradeoff.
M large
only a few levels in tree.
M small
less wasted space.
Typical M = 1000, N < 1 trillion.

Bottom line. Number of page accesses is log_M(N) per op.

When doing the tree balance, the first thing is to know "tree rotation"

Tree rotation - Wikipedia, the free encyclopedia

http://en.wikipedia.org/wiki/Tree_rotation

In the illustrated method in wiki:

OS: denote the side where we want to do the rotation -- original side -- in the example -> left side

RS: denote the purpose side that we are going to move to ---  in the example --> right side

Pivot = Root.OS       ( let Pivot point to P )
Root.OS = Pivot.RS    ( P->right, which is B is assigned to Q->left )
Pivot.RS = Root       ( Q is assigned to P->right )
Root = Pivot          ( Now, P becomes Root ) 

- When a subtree is rotated, the subtree side upon which it is rotated decreases its height by one node while the other subtree increases its height. This makes tree rotations useful for rebalancing a tree.

- When rotating the tree, the in-order traverse will not be changed:

Lefttree:((A, P, B), Q, C) Right tree: (A, P, (B, Q, C))

- To balance the tree: After rotation, the side of the rotation (destination side: RS) will increase its height by 1, while the original side (OS) will decrease its height by 1. So, one can strategically apply rotations to nodes whose left child and right child differ in height by more then 1 ( by compute the tree balance index), whereby the self-balancing tree will be helpful/

http://en.wikipedia.org/wiki/Self-balancing_binary_search_tree

Other Refs:

http://stackoverflow.com/questions/133610/balancing-a-binary-tree-avl

www.cs.princeton.edu/~rs/AlgsDS07/09BalancedTrees.pdf

# Several "Balanced" Tree 

self-balancing tree   http://en.wikipedia.org/wiki/Self-balancing_binary_search_tree

Implementations

Popular data structures implementing this type of tree include:

• AA tree
• AVL tree                         --> Important
• Red-black tree                --> Important
• Scapegoat tree
• Splay tree
• Treap

# 2-3-4-trees

2-3-4 tree. Generalize node to allow multiple keys; keep tree balanced.

Perfect balance. Every path from root to leaf has same length.

Allow 1, 2, or 3 keys per node.

2-node: one key, two children.

3-node: two keys, three children.

4-node: three keys, four children.

(Note that when adding node, -- will have splitting problem)

Search.

 - Compare search key against keys in node.

 - Find interval containing search key.

 - Follow associated link (recursively).

# Red-black trees

http://en.wikipedia.org/wiki/Red_black_tree

http://stackoverflow.com/questions/3270543/red-black-tree-for-sorting

http://stackoverflow.com/questions/2573261/red-black-tree-construction

To construct the Red-black tree

http://ocw.mit.edu/OcwWeb/Electrical-Engineering-and-Computer-Science/6-046JFall-2005/VideoLectures/

Note that, when inserting, always insert new node as black node and then proceed to the necessary correction (repainting and /or rotating)

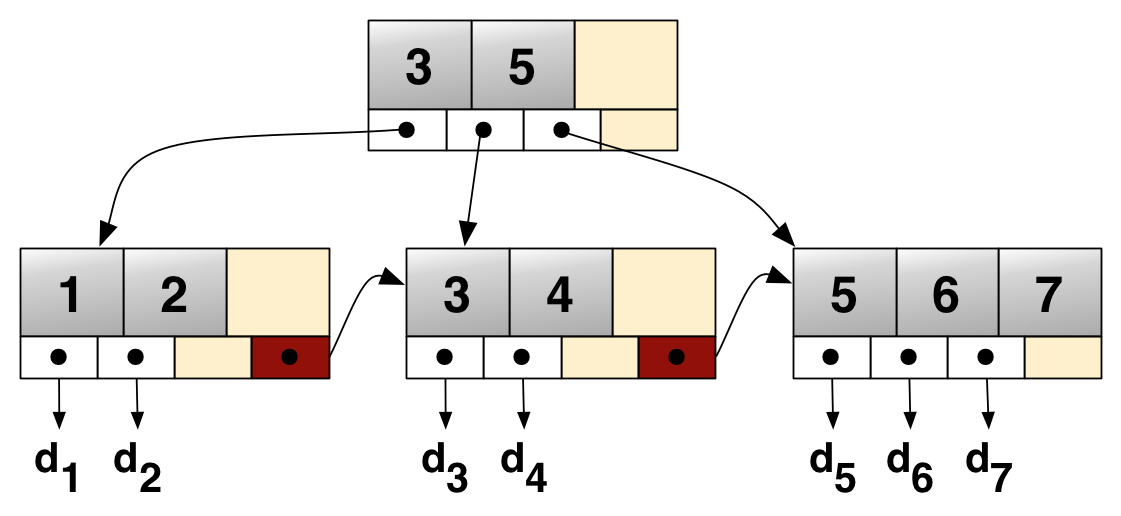
# B+trees

 B+ tree, which is one where the leaf nodes of the tree are chained together in the form of a linked list. 

B+ tree or B plus tree is a type of tree which represents sorted data in a way that allows for efficient insertion, retrieval and removal of records, each of which is identified by a key. It is a dynamic, multilevel index, with maximum and minimum bounds on the number of keys in each index segment (usually called a "block" or "node"). In a B+ tree, in contrast to a B-tree, all records are stored at the leaf level of the tree; only keys are stored in interior nodes.

The primary value of a B+ tree is in storing data for efficient retrieval in a block-oriented storage context—in particular, filesystems. This is primarily because unlike binary search trees, B+ trees have very high fanout (typically on the order of 100 or more), which reduces the number of I/O operations required to find an element in the tree.

# B-trees

http://en.wikipedia.org/wiki/B-tree

 B-tree is a tree data structure that keeps data sorted and allows searches, sequential access, insertions, and deletions in logarithmic amortized time. The B-tree is a generalization of a binary search tree in that a node can have more than two children. (Comer, p. 123) Unlike self-balancing binary search trees, the B-tree is optimized for systems that read and write large blocks of data. It is commonly used in databases andfilesystems.

# Balanced Tree Short Summary:
Red-black trees:
widely used as system symbol tables

Java: java.util.TreeMap, java.util.TreeSet.
C++ STL: map, multimap, multiset.
Linux kernel: linux/rbtree.h.

B-Trees:
widely used for file systems and databases
Windows: HPFS.
Mac: HFS, HFS+.
Linux: ReiserFS, XFS, Ext3FS, JFS.
Databases: ORACLE, DB2, INGRES, SQL, PostgreSQL