Notes on Suffix tree

# From wiki <http://en.wikipedia.org/wiki/Suffix_tree>

# A good explanation : <http://marknelson.us/1996/08/01/suffix-trees/>

# A very nice tutorial on Suffix tree <http://www.cise.ufl.edu/~sahni/dsaaj/enrich/c16/suffix.htm> 

Have You Seen This String? 

The Suffix Tree 

Let's Find That Substring 

Other Nifty Things You Can Do with a Suffix Tree 

How to Build Your Very Own Suffix Tree 

Exercises 

References and Selected Readings 

# String Search Algorithm: http://en.wikipedia.org/wiki/String_search#Index_methods

[Applications]

> longest repeated substring problem:

http://en.wikipedia.org/wiki/Longest_repeated_substring_problem

The longest repeated substring problem is finding the longest substring of a string that occurs at least twice. This problem can be solved in linear time and space by building a suffix tree for the string, and finding the deepest internal node in the tree. The string spelled by the edges from the root to such a node is a longest repeated substring. The problem of finding the longest substring with at least k occurrences can be found by first preprocessing the tree to count the number of leaf descendants for each internal node, and then finding the deepest node with at least k descendants.

Solutions from Sartaj Sahni

Find the longest substring of S that appears at least m > 1 times. This query can be answered in O(|S|) time in the following way:
(a) Traverse the suffix tree labeling the branch nodes with the sum of the label lengths from the root and also with the number of information nodes in the subtrie.
(b) Traverse the suffix tree visiting branch nodes with information node count >= m. Determine the visited branch node with longest label length.

Note that step (a) needs to be done only once. Following this, we can do step (b) for as many values of m as is desired. Also, note that when m = 2 we can avoid determining the number of information nodes in subtries. In a compressed trie, every subtrie rooted at a branch node has at least two information nodes in it.

[Some Notes]

An example of Surfix Tree:

<http://www.cise.ufl.edu/~sahni/dsaaj/enrich/c16/suffix.htm#search>

 
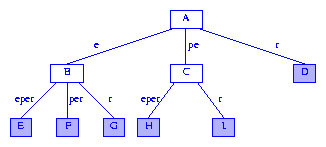
Figure 4 A more humane drawing of a suffix tree

A fundamental observation used when searching for a pattern P in a string S is that P appears in S (i.e., P is a substring of S) iff P is a prefix of some suffix of S. 

Let's take the above figure as an example, 

if follow A->C->H : pe is the prefix of eper

[Some Related Codes]

• Suffix Trees by Dr. Sartaj Sahni (CISE Department Chair at University of Florida)
• Suffix Trees by Lloyd Allison
• NIST's Dictionary of Algorithms and Data Structures: Suffix Tree
• suffix_tree ANSI C implementation of a Suffix Tree
• libstree, a generic suffix tree library written in C
• Tree::Suffix, a Perl binding to libstree
• Strmat a faster generic suffix tree library written in C (uses arrays instead of linked lists)
• SuffixTree a Python binding to Strmat

More specifically:
- Create a suffix tree from the string
- Use a Depth First Search to recursively visit nodes, starting at the root, and cumulatively adding the number of characters along edges
- The longest repeated substring is the deepest node with at least two descendants (repetition is represented by any node with at least two descendants)

Using the Suffix Tree, below are the problem it can solved:

http://www.allisons.org/ll/AlgDS/Tree/Suffix/

String Search

Searching for a substring, pat[1..m], in txt[1..n], can be solved in O(m) time (after the suffix tree for txt has been built in O(n) time).

Longest Repeated Substring

Add a special ``end of string'' character, e.g. `$', to txt[1..n] and build a suffix tree; the longest repeated substring oftxt[1..n] is indicated by the deepest fork node in the suffix tree, where depth is measured by the number of characters traversed from the root, i.e., `issi' in the case of `mississippi'. The longest repeated substring can be found in O(n) time using a suffix tree.

Longest Common Substring

The longest common substring of two strings, txt1 and txt2, can be found by building a generalized suffix tree for txt1 andtxt2: Each node is marked to indicate if it represents a suffix of txt1 or txt2 or both. The deepest node marked for both txt1and txt2 represents the longest common substring.
Equivalently, one can build a (basic) suffix tree for the string txt1$txt2#, where `$' is a special terminator for txt1 and `#' is a special terminator for txt2. The longest common substring is indicated by the deepest fork node that has both `...$...' and `...#...' (no $) beneath it.
(Try it using the HTML FORM above.)
Note that the `longest common substring problem' is different to the `longest common subsequence problem' which is closely related to the `edit-distance problem': An instance of a subsequence can have gaps where it appears in txt1 and in txt2, but an instance of a substring cannot have gaps.

Palindromes

A palindrome is a string, P, such that P=reverse(P). e.g. `abba'=reverse(`abba'). e.g. `ississi' is the longest palindrome in `mississippi'.
The longest palindrome of txt[1..n] can be found in O(n) time, e.g. by building the suffix tree for txt$reverse(txt)# or by building the generalized suffix tree for txt and reverse(txt).
(Try it.)

Others 

--
http://www.cs.helsinki.fi/u/ukkonen/SuffixT1withFigs.pdf

♥ ¸¸.•*¨*•♫♪♪♫•*¨*•.¸¸♥